Software/Firmware Subsystem
TLDR
Check out our Github repository at https://github.com/liloheinrich/Swerve.
Here is a list of dependencies required:
- Python libraries: socket, serial, numpy
- Arduino libraries: Serial, Adafruit_NeoPixel, Servo
- RaspAP for simple wireless network setup
Communications
We use the python serial library to communicate between the laptop and joystick as well as the Arduino serial library when communicating between the Pi and Arduinos, since each of these devices connects via USB. To communicate between the laptop and the Pi we use the socket library to connect and read from a network socket, and to set up the wireless router we used RaspAP. The main tutorials we followed include Raspberry Pi Socket Protocol and How to get USB Controller Gamepad to Work with Python for USB gamepads, as well as the Arduino Forum’s Serial Input Basics.
The format of the messages sent between devices is as follows:
- Laptop → Pi message: [left_joystick_x, left_joystick_y, right_joystick_x]
- Pi → Arduino message: [motor_1_speed, motor_2_speed, servo_1_angle, servo_2_angle]
Laptop/Joystick Code
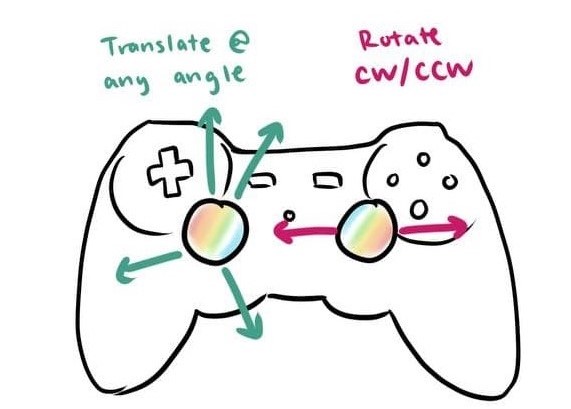
To interpret the left joystick (translation) reading as x and y components, we correct for the square shape of the input values and map it onto a circular space which matches the movement range of the physical controller. This can be done using the following line of code that maps x and y each in the range [-1.0,1.0] onto a circular space by scaling each of the components:
def map(x, y):
return x * math.sqrt(1 - y*y/2.0), y * math.sqrt(1 - x*x/2.0)
The math behind this is explained very well in this blog post by Robert Eisele.
Raspberry Pi Code
The Raspberry Pi computer does the main “thinking” and math calculation in our system. On the Pi we have two important files: swerve.py which is the main file and drive.py which handles the math. We additionally used servo_calibration.py as a simple program which allows us to align all of the modules.
servo_calibration.py
This file is used for calibration to align all of the modules so that they face in the same direction. Once the array `servo_angles_ranges` containing each minimum and maximum servo angle is adjusted correctly, those values are directly transferable to swerve.py and the robot is able to orient its wheels correctly.
swerve.py
This is the main file that runs the communications, data parsing and sending, and remaps servo angles to their adjusted range.
drive.py
This file handles the vector math that goes into mapping the joystick controls to our desired behaviors, outputting the servo angle and motor speed to set each module to.
In the drive() function we essentially add the translation and rotation vector together for each module. For example, to rotate clockwise, the modules must each drive at a different angle pointing tangent to the midpoint of the robot. On the other hand, to translate, all of the wheels must point the same way. To combine both motions, the translation and rotation vectors are added together and scaled back into the valid range.
x_rot_bymodule = np.divide([-1,-1,1,1], math.sqrt(2.0))
y_rot_bymodule = np.divide([-1,1,1,-1], math.sqrt(2.0))
# inputs:
# x_s - left joystick x-axis value on range [-1.0, 1.0]
# y_s - left joystick y-axis value on range [-1.0, 1.0]
# r_s - right joystick x-axis value on range [-1.0, 1.0]
# outputs:
# res_mag - resulting vector magnitudes aka motor speeds on range [-1.0, 1.0]
# res_ang - resulting vector angles aka servo angles, int() on range [-90, 90]
#
def drive(x_s, y_s, r_s):
# turn r_s into magnitude and angle
r_dir = getsign(r_s)
r_mag = abs(r_s)
# calculate x and y scaled vector components of the rotation
x_r = x_rot_bymodule * r_mag
y_r = y_rot_bymodule * r_mag
if not r_dir: # flip rotation vectors if counterclockwise
x_r *= -1
y_r *= -1
# add x and y vector components of translation and rotation together
res_x = [x_s + x_r[i] for i in range(len(x_r))]
res_y = [y_s + y_r[i] for i in range(len(y_r))]
# convert x and y components to magnitude and angle
res_mag = [math.sqrt(res_x[i]**2 + res_y[i]**2) for i in range(4)]
res_ang = [math.atan(res_y[i] / res_x[i]) for i in range(4)]
# scale magnitudes back into -1.0 to 1.0 range in case
if any([abs(r) > 1.0 for r in res_mag]):
max_mag = max(res_mag)
res_mag = [(m / max_mag) for m in res_mag]
# scale angles back into -90 to 90 degree range - reverse motors if necessary
if any([a > 90 for a in res_ang]):
res_ang = [a - 180 for a in res_ang]
res_mag = [-m for m in res_mag]
# gives motor speed (-1.0 to 1.0), servo angle (-90 to 90 degrees)
return res_mag, res_ang
Arduino Code
We decided to make the two-Arduino system symmetrical to prevent confusion: the same file is compiled and run on both Arduinos. To enable this, we assigned a symmetrical pinout for the servos and motors, but then flipped the motor signal wires for forward and reverse in order to make forward rotation the same for all motors under the same code. Another note about the arduino code is that we had to scale the maximum motor speed down to one-quarter (64 out of the maximum 256 duty cycle) because the driving motors go quite fast with a high RPM and only a 3:1 gear ratio.
run.ino psuedocode:
void setup() {
begin serial
attach servos to PWM port
set motor PWM pins to output mode
set all motor speeds to zero
begin neopixels
set all neopixels in each strip to specified color
}
void loop() {
if (there is data available on serial) {
receive message between the start and end markers into the buffer
if (a valid message was received into the buffer) {
parse the buffer to get the two motor speeds (floats) and two servo angles (integers)
analog write to the servos to turn to specified angles
analog write to the motors to execute the specified velocities (scaling down to 0.25x)
}
}
}
Test Programs
In addition to the files mentioned, along the way we also wrote several other test programs (which can be found in our repository) for things such as:
- Moving the servos and motors
- Serial and socket communication tests
- Testing out just one swerve module or all modules driving in a straight line
- Testing out the gyro (not working)
- Visualizing drive() vector addition using pygame / matlab