Symbol Recognition

The Symbol recognition is performed in two parts. First, an ESP32-Cam captures a frame of the physical tape in real-time which is a single bit (0 or 1). We create bit-strings of 3 bits each, and these bit-strings are mapped to the six symbols (our alphabet for the Turing Machine) we have for the Turing Machine to perform computation.

The mapping for the bit-strings to symbols is as follows:
000 -> #
010 -> 0
011 -> 1
101 -> X
110 -> Y
111 -> _

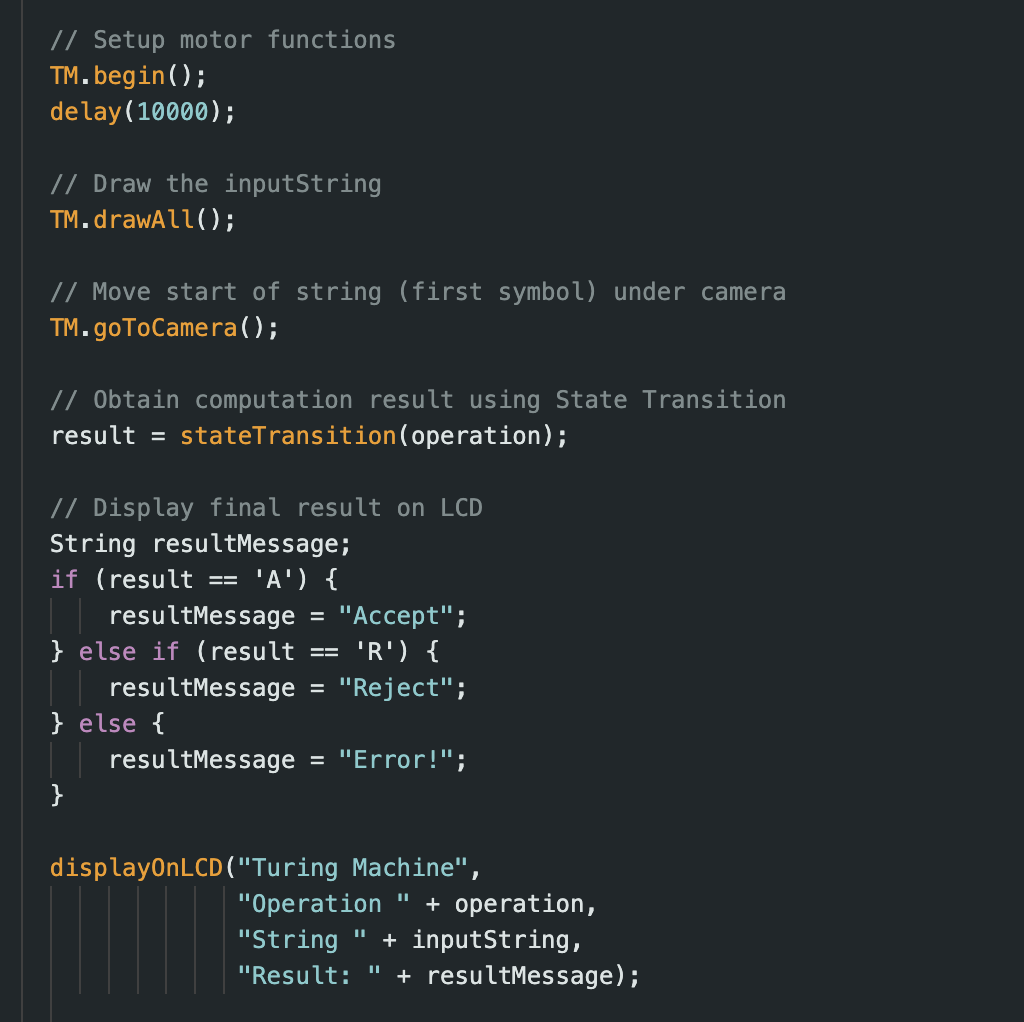
Firmware: Symbol Writing and Erasing

The firmware to write/erase symbols is pretty straightforward as we have functions to draw symbols, erase symbols, etc. which take use of more abstract functions like draw a bit 0, etc. All the functions are abstractly made from basic motor controls based on the desired functionality required. These functions work in sync to perform writing/erasing based on the state transition rules for an operation while performing a computation on the Turing Machine.

State Transition

The state transition is performed based on which operation needs to be performed on the Turing Machine. As our model is based on the idea of a Universal Turing Machine, it is capable of performing multiple operations on the same machine and has different sets of rules (or instructions/transitions) to perform these computations.

In a Turing Machine, we track the current state and the current symbol, and then based on the operation and set of instructions, we determine the state to transition to, the symbol to write at the current position, and whether to move one symbol forward or backward (which translates to moving the pointer either (+1 or R) or (-1 or L) in a theoretical Turing machine).

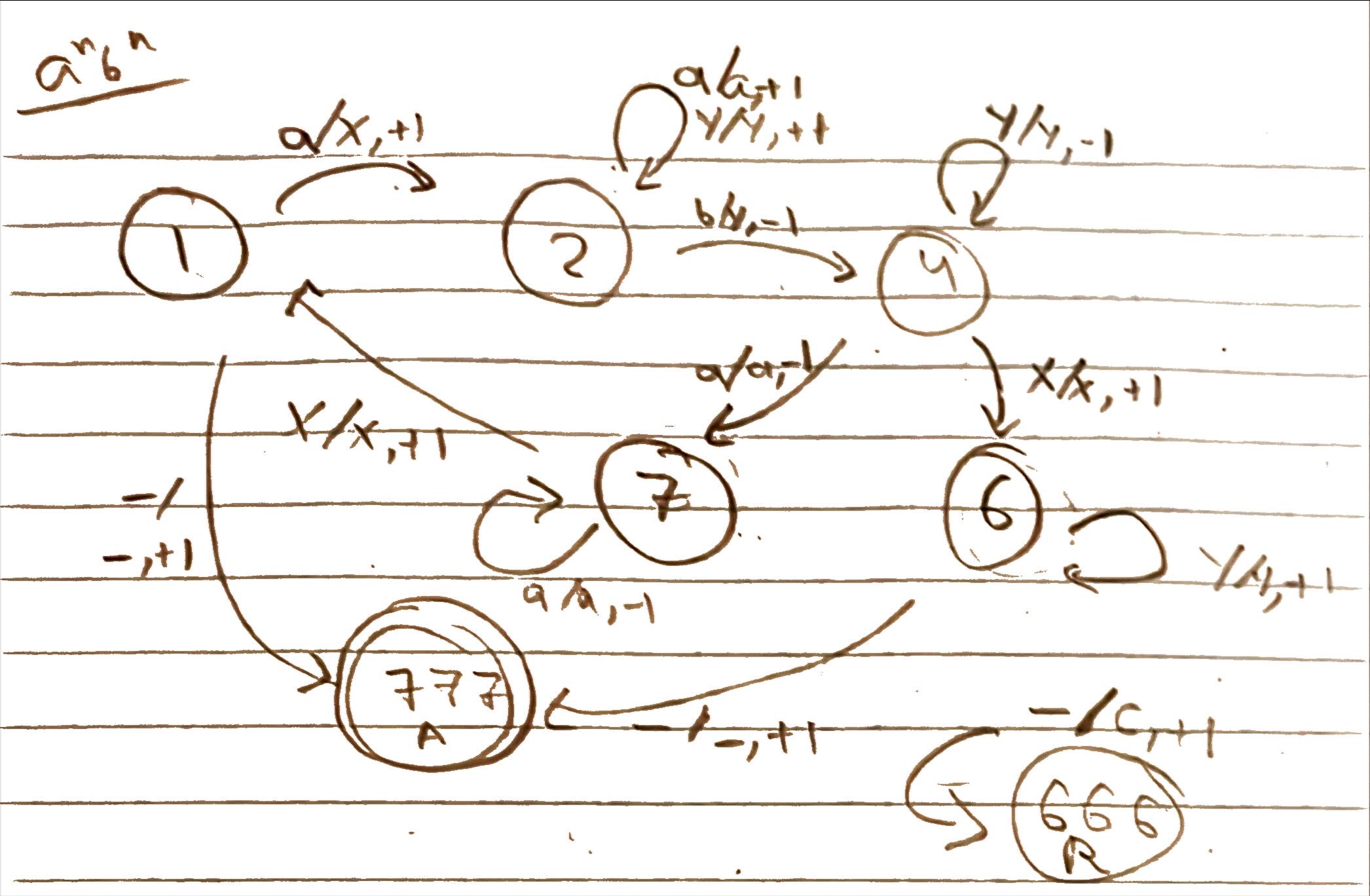
The state transition rules are determined by creating state diagram for different operations which basically indicate the states and how the rules work. The diagrams vary in size based on how complicated an operation is and how many states it utilizes.

The image here is a sample state diagram for the operation of checking whether a string has an even number of a's and b's (same as having an even number of 0s and 1s).